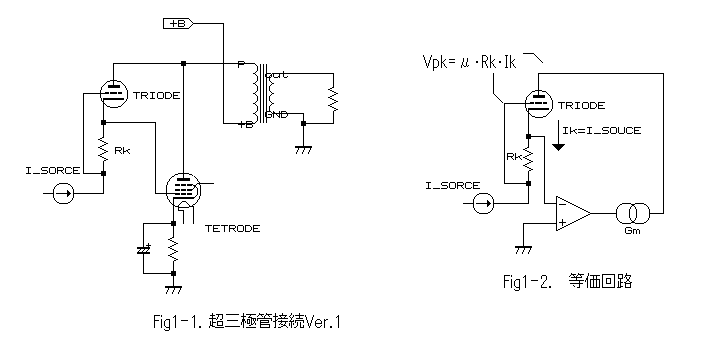
The Super Triode Connection Ver.1
- For the transistor generation -
The Super Triode Connection (STC), invented by
Shinichi Kamijo, uses triode as feedback path device instead of a resistor
as conventionally. By this method the STC adopts the triode's performance
characteristics, so you get the sonic of the triode used with a low plate
resistor, even if you actually are employing a pentode, beam deflection tetrode
or even a transistor, as power output (current amplification) device.
Kamijo-san's home page is here.
Shinichi Kamijo invented several types of STC, but here I focus on the
Version 1 type, because it exemplifies the basic idea underlying all STC
types. I think you can readily understand the others if you understand the
Ver.1 topology.
In addition, probably you may feel the STC-MX
(my original idea) is complicated, but if you can understand the Ver.1 basics,
then you may find it is not actually very difficult.
However, understanding the STC topology may not be so easy for the younger generation, because young people versed in semiconductor based technology do not properly know how tubes and tube circuitry work. I believe one of the biggest problems is the triode itself, because it is a voltage output device, whereas the transistor is a current output device.
Furthermore, the STC uses the triode as a feedback path device. This is a very unusual way to use a triode. Therefore, here I explain the STC from the point of view of people who understand transistors.
The figure below shows the basic schematic of an STC amplifier, and that at below-right is the equivalent circuit. In this circuit, probably those of the transistor age cannot easily understand this "triode feedback".

I will not explain the tetrode or pentode function here, because these devices have similar characteristics to comparable semiconductor devices (e.g. depletion mode FET's). In short, it is enough if you can understand that they are current output devices.
First of all, in order to understand the STC, you need to know how a triode actually works. If you are familiar with transistors, suspect that you are used to thinking about the device working in terms of current. But here you have to think about it in terms of voltage instead of current.
There is a 'heater' inside of the cathode, and it heats red-hot. The heater heats the cathode to cause it to emit electrons. Electrons are energized by the heat resulting in this emission effect. Therefore, in order to increase those electrons - in other words to increase the current - heater needs to spend much more power.
As you know, an electron has a minus electrical charge, so electrons will be attracted if there is plus charge in proximity. This is the role of the plate of the triode tube. As a result, "electron current" flows from cathode to plate. (But "conventional current" flows from positive to negative, so the resultant tube (conventional) current is described as flowing from plate to cathode).
The GRID can be used to control this current flow. To do so, the grid potential is set-up (“biased”) such as to be negative with respect to the cathode. The plate is set up with a high positive voltage potential, so the negatively charged electrons emitted from the cathode, go to the plate, but are interrupted by the effect of the voltage at the grid. Therefore, the (conventional) current flow from plate to cathode is controllable by the grid.
The grid is at no particular voltage level at all, until external resistors or voltage references are connected to the grid and to the cathode. The grid must be "biased" by these means, to properly enable control of the cathode-plate current. Free of any control by the grid, the tube is naturally conducting very significantly. Most bias arrangements therefore always act to "back off" this natural cathode-plate current flow; the grid is thus almost always operated ("biased") with negative voltages, with respect to the cathode. The tube is like a JFET in this regard, and not like a MOSFET or bipolar transistor at all, where "bias" is typically "forward" and involving positive control element voltages.
Negative voltages at the grid, which is physically in close proximity to the cathode, inhibit the emission of electrons, being also negatively charged, from the cathode. The more negative the grid, the more electron flow from cathode to plate is inhibited, the less current flows. The less negative the grid, the more cathode-plate (electron) current can flow.
The grid must be "biased" by either;Therefore, the current flow from plate to cathode is controlled by the grid.
(a) "fixed bias" = application of external minus DC supply to the grid, with cathode grounded, or
(b) "cathode bias" (also called "self bias") = cathode caused to be positive relative to the grid (that is to say "grid minus relative to cathode" again), by adding a resistor in series with the cathode (to ground). The natural flow of plate-cathode current in the tube itself creates the bias voltage. It is also necessary to return the grid to ground via a (typically very high value) resistor, for this bias to work.The STC Ver.1 uses method (a) for bias for the feedback triode*, and output tetrode/pentode is method (b). But in the case of the feedback triode, controlling current through the feedback triode’s cathode resistor (Rk in Figure 1) not only sets up static bias, but is also the means for applying audio signal drive too.
(*Note: Please be care, the topology of feed-back triode is similar to self-bias, but the bias voltage is clearly "fixed" if no audio signal. "Fixed bias " does not mean the topology, but the "method" to decide the bias voltage.)
At the same time, if the plate voltage potential is deliberately raised, the electrons from the cathode will be attracted more strongly, and the current flow is increased. So, as a result, both the plate to cathode voltage (Vpk) and the grid to cathode voltage (Vgk) can change (control) the current flow. So the plate to cathode current Ik(=plate current Ip) increases or decreases in proportion to the Vpk and the Vgk;
Ip = C0·Vpk, and Ip = C1·Vgk : Here C0 and C1 are proportional constant.The proportional constant C0 is usually referred to by its inverse function conventionally, which is termed 'rp' (plate resistance);
Ip = (1/rp)·Vpk = Vpk/rpAnd the proportional constant C1 is termed 'gm' ("transconductance");
Ip = gm·VgkPlease remember these relationships.
With the plate directly connected to some positive voltage, one must imagine that there is this imaginary internal plate resistor 'rp' between that positive voltage and the plate. This is quite different behaviour to pentode, tetrode and indeed transistor behaviour.
It means that the plate voltage Vpk will change if the "infinite load" is connected to plate or cathode, because Vgk changes the plate current Ip, and the voltage is defined by the internal resistance 'rp' .
Vpk = C2.VgkSo now the plate to cathode voltage is also controlled by Vgk, not just the plate current Ip. The proportional constant between Vgk and Vpk (C2) is called 'mu'.
Vpk = mu·VgkOr, put another way;
mu = Vpk/VgkNow all these equations shown above may be simply combined;
Ip = Vpk/rp = gm·VgkRearranging a little, gives the basic equation describing the performance of a triode;
Vpk/Vgk = gm·rp = mu (a constant)An implication of this is that when current Ip passes through the internal plate resistance rp, some voltage will be dropped by that rp. For most other active devices (pentodes, transistors) this internal or "source" resistance is considered almost infinitely high, and changes in Ip (or its equivalent) produce hardly any such internal changes in voltage at the plate (or collector) etc. That is to say, these other devices have an internal plate/collector characteristic like a "current source".
In the case of the triode however, if rp were low enough, the output characteristics of the plate will be akin to a voltage source rather than a current source. This is the biggest difference between semiconductor.
Please consider now the graph shown below. This is called the 'plate characteristic' diagram, as it shows the relationship between Ip and Vpk and Vgk. (Note that this particular diagram is idealized; it shows the characteristic of an ideal triode, not necessarily a real-world one!)In conclusion, let us restate and summarize the equations of the triode;
- The voltage Vpk changes according to Ip if passing through rp, so;
Ip·rp = Vpk.
- mu is the proportional constant between Vgk and Vpk, so;
Vpk = mu·Vgk.
- gm is the proportional constant between Ip and Vgk, so;
Ip = Vgk·gm.
- Therefore, mu = rp·gm.
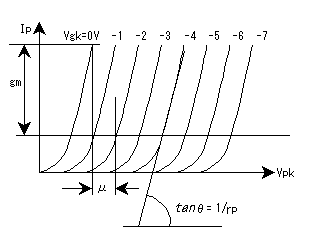 Figure 2. Triode characteristics
Figure 2. Triode characteristics You can easily to understand that Vgk will control the plate voltage Vpk,
but note that each of the three parameters shown will affect the others.
This graph shows these basic relationships.
The parameters mu, rp and gm may be derived from these curves.
• rp = Vpk/Ip is the inverse of the slope of the Vgk lines. So rp is the tangent ratio of the angle (theta) shown on the diagram.
• Gm = Ip/Vgk, so is shown as the change on the vertical (Ip) axis (marked in the diagram) per unit change in Vgk (the change from Vgk = -1V to Vgk = 0V as shown).
• mu = Vpk/Vgk, so is the change in Vpk on the horizontal axis per unit change in Vgk (shown as the change from Vgk = -1V to Vgk = -2V on the diagram).
Now let us consider the operating conditions, specifically the load line, for the feedback triode (not the overall amplifier). Maybe you have previously learned that the angle of the load line gives the resistance value of the load. But this is not always so. The load line of the feedback triode is not defined by a load resistance, but by a "current source signal".
Firstly, I will explain the "current source signal".
To start with, recall that a VOLTAGE source signal, which perhaps you are more familiar with seeing, has (in theory at least) zero source impedance. This says that the source voltage follows the audio signal absolutely, independently of the load. High impedance load, or low impedance load, the signal source supplies however much current is demanded. And (again "in theory"), the audio signal voltage is never changed by such loading.
That is a "voltage source signal". A "current source signal" is just the opposite!
A CURRENT source signal has infinite source impedance ("in theory"). This says that the source current follows the audio signal absolutely, independently of the load. High impedance load, or low impedance load, the signal source supplies whatever voltage level is demanded such as to drive that current. The audio signal current is never changed by such loading.
An alternate way to look at the "current source signal" is to imagine the more familiar "CCS" or "Constant Current Source". This outputs a constant current, independent of the load circuit it feeds. But then imagine that the actual value of CCS current is not absolutely fixed, but is able to be modulated. Now let the audio signal be the CCS current value "control signal".
In the STC Ver. 1, the cathode of the feedback triode is connected to a "current source signal". The current source signal has near-infinite source impedance value. So the current flow through the feedback triode will be determined solely by this current source value. In this case, the current through the feedback triode is "independent" of the internal plate resistance, rp.
Another outcome of the current source signal having effectively an infinite internal (source) impedance, is the feedback triode’s plate-cathode current flowing at a constant level (albeit with modulation due to the audio signal). This means that whatever voltage potential appears at its cathode depends (using Ohm’s Law) on;
(a) the current source signal μA or mA value, moment by moment, andThe (effective or dynamic) source impedance of a practical current source signal can be expected to be, and treated as, effectively infinite in value.
(b) the load resistance connected to it. Whether a low resistance or a high resistance, even a "Meg-Ohm" resistor, the voltage at the current source output is always just (a) x (b).
To recap then, the "current source signal" means that the current source’s actual μA or mA value is modulated by the audio input signal. This is the equivalent action of a pentode, tetrode (or FET) as the input device, because if you connect the grid of a pentode or tetrode to the input signal voltage, then the plate current will be modulated by that signal voltage, (the plate being treated as having near-infinite source impedance).
Let's now think about the load line of the STC and its actual manner of operation here. The most important feature is the feedback triode. It is connected between the plate and the cathode of the output tetrode/pentode tube. This triode provides the 'feedback path' for the output tube's plate to grid negative feedback(NFB). I will explain how it works in this feedback mode, shortly.
Given that you now already understand how the triode actually works, I'll
explain the feedback triode of the STC with the aid of the example shown below.
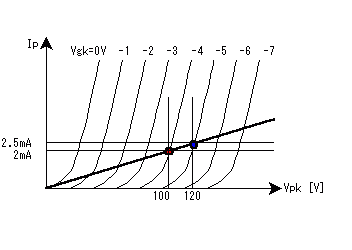 Figure 3; load line
Figure 3; load line
Initially, let the plate current of the triode be 2mA, with Vgk is -4V,
meaning that Vpk is 100V. This is indicated by the left-hand point (red)
on this Figure.
Look now again at the equivalent circuit shown in Figure 1. In Figure
1, Ik = I(Rk) = I_source.
Basically, the grid of a tube has a very high input impedance, so the grid current(s) can be safely neglected, and so Ip =Ik. This Ik is the Ip in Figure 3.Vpk = Ip·Rk, so the Rk has to be 2kohms, i.e. 4V ( as Vgk) divided by 2mA (as Ip = Ik).
Now we can be sure that Vgk will be zero if the Ip is zero, since no Ik means no voltage developed across Rk. So the load-line for the feedback triode has to pass through the origin (zero-zero point on the graph).
Let now the Ip increase to 2.5mA, (say due to the input signal drive). Let's initially assume the plate potential stays the same. But Vgk will change; the value of Vgk must become 2kohm x 2.5mA = -5V.
This is indicated as the right-hand point (blue) in Figure 3. Now from
this diagram, Vpk has to now be 120V, if Ip is 2.5mA and Vgk is -5V.
But the plate potential (relative to chassis ground, 0V) was defined as
"unchanged", so instead the cathode potential must change; the cathode potential
must drop. (It is impossible to change the plate voltage by the small feedback-triode
current, because the load resistance is too small for that current.)
Now the cathode of feedback triode is connected to the grid of output tube and the current signal source, so the grid of output tube potential is unsettled. By changing feedback triode cathode potential, Vpk will be 120V.
Basically, the output current Ip of the output tetrode/pentode is determined only by its Vgk. Since this grid bias on the output tube will become more negative, less plate current Ip will flow in it. It's Its plate voltage will tend to rise. Vp (the plate voltage relative to chassis ground, 0V) of the output tetrode/pentode will rise toward 120V.
Now look at Figure 1 again.
The output current of this amplifier is only defined by the triode Vpk,
the feedback voltage, because the grid voltage of the output tetrode/pentode
is not fixed, but floating, since the input signal 'I_source' is a current
(not a voltage).
For this reason, only the feedback voltage determines the grid voltage of
output tetrode.
This character is called 100% voltage feedback, because the input impedance (the source impedance of a CCS) is infinite, while the feedback resistor has some defined, real value, being the rp of the feedback triode.
This operation is similar to that of a high gain operational amplifier.
OK, now let's get back to the load-line. The load-line passes through both the points marked and zero-zero on Figure 3. This is the load-line for the feedback triode, but not the complete amplifier.
The input signal of the amplifier is a current, not a voltage. We can
say that the output voltage will be changed by the input signal current working
the feedback triode along its load-line.
I write that the output voltage will be changed, but of course the feedback
is not superconductivity(!), so the output has some output impedance.
The value of output impedance is determined by the characteristic of output
tetrode.
As I already explained, this is 100% voltage feedback, so it is defined
by the trans-conductance (gm) of output tetrode, because it defines the open
voltage gain.
Ip of tetrode/pentode is determined by Vgk and proportional constant 'gm'
(transconductance);
Ip=gm·Vgk, so Vgk=Ip/gmSo, if the load resitance(or impedance) is RL, the open loop voltage of tetrode;
Vout=RL·Ipgain of tetrode Av is Vout/Vin. From above two equations;
Av=gm·RLAnd thus, the output impedance Ro is determined by 100% feedback,
Ro=RL/(gm·RL) = 1/gmthis is just the same as cathode follower.
If the gm of the output tube is higher, then the open-loop gain, gm.RL as above, will higher. The feedback will therefore also be increased (as there is 100% voltage feedback), and so the output impedance becomes lower.
Now, we can look at the characteristic of whole STC amplifier. As
I already explained, an output impedance is the angle of plate characteristics
lines, and it is the proportional constant of Vpk and Ip.
I previously explained how, for a triode, source or output impedance rp
is given by Vpk/Ip which is the inverse of the slope of the Vgk lines seen
in Figure 2; rp is the 1/tan of the angle (theta) shown on the Figure 2 diagram.
The characteristic of the whole amplifier may be considered in a similar, parallel way. Instead of "rp" for the triode, instead consider "Ro" (and Ro = 1/gm) for the characteristic of the complete amplifier.
Therefore, the characteristic of whole amplifier can be approximated by the slanting linear lines, the angle of the line is 1/gm. The amplitude factor has to be the same as feedback triode, so it has to be mu, but this is not real amplitude factor but the current to voltage conversion factor.
The below graph is the load line of RL and characteristics of whole amplifier. Please notice, slanting lines are not defined by the input voltage, but by the input current (Ik). This is the characteristic of STC Ver.1.
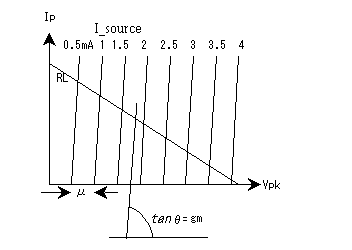 Figure 4: Overall characteristics of the STC Ver. 1
Figure 4: Overall characteristics of the STC Ver. 1
Of course, you have to define the RL from the raw characteristics of output tetrode/pentode. Generally speaking, this character is further constrained and defined by the knee point, maximum current and maximum plate dissipation of the output pentode.
As the feedback is not the magic, the original characteristics of the
output tetrode/pentode are not changed by the feedback.
The STC amplifier overall characteristic is achieved by controlling the
grid voltage of the output tube such as to take on the characteristics of
the feedback triode.
In other words, Vpk of the feedback triode is defined by its mu, so the grid voltage of the output tetrode/pentode is controlled to achieve the same character automatically.
The last step is that we have to define the input current, I_source = Ik.
If you are familiar with semiconductors and their theory of operation, then
this is easy to do.
For instance, if you use a transistor for the input device, you can determine
an appropriate emitter resistor from knowing the maximum input voltage.
The output (collector) current of this transistor will be defined by that
emitter resistor.
This is the simplest method, but is typically sufficient.
* Special thanks; Paul.
Last update 5th/Nov./2002