から、(1)式は
周波数特性について。
ここでは、任意のシステムに関する周波数特性の計算手法を考えます。
その為には、そのシステムの伝達関数なりδ応答なりフーリエ変換なりが解っている必要があります。
ここでは、ラプラス変換の所で出てきた(5)式を例にします。
これにs=jω を代入して得られる関数は、この積分回路の複素周波数特性です。
これを、通常使われる振幅と位相にするにはどうすれば良いか?考えて見ることにします。
オイラーの公式
![]()
から、(1)式は
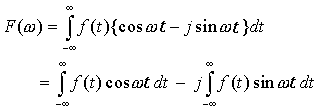
f(t) は、通常は実関数 (残念なことに、私は虚数の音というのは聞いたことがない
^^;) ですから、この式のcos部分が実部、sin部分が虚部です。
複素平面というのは、実軸と虚軸が直交しているのですから、直角三角形の二辺から他の一辺の長さを求める問題です。(下図 Fig4参照)
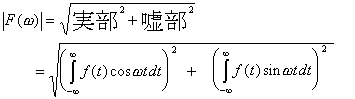 (6)
(6)
これが周波数振幅特性、オーディオ業界では俗に f
特
と言っている奴です。
つまり、周波数特性=振幅じゃないって事です。周波数特性にはAmplitude:振幅とPhase:位相があります。
振幅のみを取り上げて f 特なんて言葉を使うのは、オーディオ業界以外では通用しません。
評論家といわれるエライ諸先生方の勘違いが原因でこうなったんじゃないかと、私は思ってます。
振幅特性を簡単に求めるには、伝達関数からH(s)・H(-s)を求め、s=jω を代入してルートをとれば求まります。証明は簡単ですから、興味のある人は御自分でどうぞ。
例をあげると(5)式から
を得ます。ルートをとったら振幅(amplitude)ですが、ルートをとる前はパワーです。そのパワーが1/2になる周波数の事を、カットオフ周波数と呼んでいます。逆に言えば
![]()
としてやれば、任意のカットオフ角周波数でのR とC の積が求まります。この積RC
の事を時定数、と言います。
これは、この式(分母が一次の場合)に限って言えば、伝達関数の分母多項式が零になる周波数です。(一般的には、分母多項式が零になる値は複素数ですから、これは常に言える訳ではありません。)
伝達関数の分母多項式が零になる周波数の事を、極と言います。
分母が一次式の場合、極は当然実軸上になりますが、二次式以上では一般には複素極を持ちます。
この極の概念は特に重要で、システムの安定判別に使われます。
即ち、極がs平面で左半平面にある場合は安定、右半平面に一つでもあれば不安定、虚軸上にあれば定常発振です。
回路網理論やフィルタ理論の例でいえば、極の位置が、複素平面の零点を中心に円周上に等角度で並んでいる時が、バターワース特性(最大振幅平坦特性)です。
位相特性と群遅延時間
位相特性φ(ω)は、周波数特性の実部と虚部の比からアークタンジェントをとれば求まります。Fig.4を見て下さい。
![]()
(5)式の例では、
![]()
となります。先ほどの極の位置が左半平面にあることとの関係で例を挙げると、NFBアンプの安定度ではφがπになる角周波数で利得が1以上あれば不安定です。これらは同じ事を違う言葉で表現しているに過ぎません。有名なナイキストの安定判別とかも、結局は簡単に求めるためのもの、と言うだけで、同じ事なのです。
(8)式を周波数で微分したものが、群遅延特性になります。
つまり群遅延時間が一定であるというのは、位相特性は線形関数(直線)である、と言う事です。
間違えないで欲しいのは、線形関数であれば良いのであって、決して位相が平坦である必要はない、ってことです。
ここで、位相と群遅延時間に関して、どうも勘違いをなさっている方が多いようなので、一言述べさせて頂きます。
よく、位相が進むとか遅れるとか言いますが、位相が進む、というのは全ての周波数領域で入力より出力信号が進む事はありません。出力周波数の一部の位相が進むことはあり得ますが。
実は、オーディオにおいて全帯域で位相がどうなるかは、全く問題ではありません。全帯域で群遅延時間がどれだけ遅れようが、関係無いのです。
これは、馬鹿馬鹿しいぐらい、あまりにも当たり前なのですが、少しだけお話しましょう。
例えば、CDの音をいったんメモリーに貯えて、再生したとします。
この場合には、そのメモリーに貯えてあった時間は遅延時間ですが、これで音が変ると思う人はあまり居ないでしょう?(この遅延時間は直流を含み、群遅延特性とは少し違うけど...)
「位相が線形である」というのはこういう感じです。要は、群遅延時間が平坦(零でない一定値)であるかどうかが問題なのです。
上述の例では直流の遅れ(変な表現ですが)を含みますが、普通の場合には直流での位相回転が0°です。
よって位相歪みがないことは、即ち周波数に対して位相遅れが比例している事を意味します。
位相と群遅延の少し難しい話(ここは読まないで下さい ^^;;)
もう十分に難しいと想っている人はこれから先は読んではいけません。位相ってのは、マジで考えると難しいものです。
さて、難しい話というのは、位相と群遅延の基準についてです。
位相ってのは、基本的には±πで表します。これは、基準の取り方次第できまるような所もあります。
例えば、一次ハイパスフィルタの位相は、直流を基準に取るとしたら、周波数軸上の無限遠点で90度の位相進みです。
しかし、例えば入力に正弦波を入れて発振器の電源をオンした瞬間の波の最初の立ち上がりが入力よりも進んでいるわけがありません。勿論、少しは遅れがあります。
正弦波であっても、電源を入れた時の本当の立ち上がりというか、無信号からいきなり立ち上がる部分では、インパルス的であり、非常に高い周波数成分を含みます。その部分では高い周波数程、遅れが小さいだけです。
だから、考えようによっては、ハイパスフィルタのインピーダンスが零に近づく所での遅れが小さい、と取ることも出来ます。だから、別段これは位相が進んでいるとも遅れているともとれます。位相ってものは無次元のスカラ量ですから、基準をどこかにとっての値なんですね。
通常は直流を基準にとります。その方が考えやすいからですが、そうすると直流では零になり、高い周波数でπ/2の位相進みです。群遅延特性は位相の微分(それは位相特性の接線の傾きに過ぎない)ですから負になります。
もし低域でゆっくりとした位相遅れがあり、それが高域で急激に進めば、接線の傾きは正よりも負の値が大きくなります。
だから、これはその周波数領域では群遅延時間が負で、進んでいる状態になります。
しかし、これは信号遅延が本当に進んでいるのとは全く意味が違います。
これは位相の与え方とも、基準の取り方の問題ともいえます。同様に群遅延もこれは言えます。
先ほどCDの例をあげました。あれは確かに遅延時間ですが、逆に群遅延時間が即ち信号遅延では無いのです。
逆は成立していないので注意を要します。
位相進みは負の群遅延時間になりますが、直流を含む全帯域で位相が進むことはありません。全帯域で進むと言うことは、非常に高い周波数成分も直流付近も含み、位相が進む事です。つまり、インパルスの立ち上がり部分から位相が進む事になります。
だから直流近傍を含む全帯域での位相進みは、どこを基準にしても信号の進みになります。
それは、「タイムマシン」と言います。入力が来る前に出力が現れる事になる訳ですから。
信号処理理論では、これを「因果性を満たさないシステム」といいます。勿論、因果性を満たさないシステムは存在しません。(特殊相対性理論の要請から、最大伝送速度は光速です。光より速ければ過去に情報が送られます。)
間違ってタイムマシンなんか作らないで下さい。真空管アンプで相対性理論が崩されたんじゃたまりません。
尚、ついでに言っておくと、進みであれ遅れであれ、全帯域の一定の位相角の変化(この時、群遅延は全帯域で0)は時間波形の変化(つまり位相歪み)になります。
何故なら、直流を基準にして位相回転が1Hzで90°なら0.25秒の遅れですが、100Hzなら0.025秒ですから、全部が一斉に遅れることにはならないからです。
さらに、位相と振幅は必ずしも一定の関係を持っているわけでもありません。位相だけを変えるフィルタと言うのも存在します。両者を決定づけるものは唯一つ、複素周波数特性の実部と虚部の間にはお互いにヒルベルト変換対の関係にある、と言うことだけです。
参考までに、良く使われるNFBの位相進み補償というのは、高域でのNFB電圧の位相遅れを小さくする、という事であって、入力よりも位相を進むめるのではありません。念のため。
あぁ〜あ、読まないでって書いたのに読んじゃった。解らなくなっても私のせいじゃないよ。(^^;;)
Last Update 2001/12/17