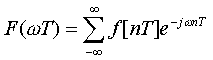FFT

フーリエ変換のページで触れたように、フーリエ変換は「連続な関数」の変換です。
ディジタル信号はサンプリングされています。これを離散信号（Discrete signal）と言います。

フーリエ変換を、サンプリングされた離散信号（つまりディジタル信号）について考えて見ましょう。

連続関数のフーリエ変換（１）式は、無限時間の積分です。積分というのは、ある関数の面積を求める作業ですね。
と言う事は、サンプリングされた信号で言えば、そのサンプリング点のみが値を持つ訳ですから、全てのサンプル値を加算すれば、それは面積を求めることと同じですよね。

つまり、積分の代わりに、サンプリング・ポイントでの無限の足し算をすればよいわけです。

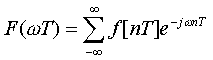　(10)

これが定義式になります。（毎度の事ながら、数学的には厳密な解釈じゃないです）T はサンプリング周期（＝1/fs）、n は整数です。
この式はｎに関する総和です。この nT を離散時間と言います。
連続な関数 f(t) を周期Ｔでサンプリングした時、f[nT] は周波数領域で±πに限定されます。
そしてfs/2で帯域制限された元のアナログ波形は、sinX/X で補間すると再現されます。所謂サンプリング定理です。
　

FFT はFast Fourie Transform (高速フーリエ変換）の略ですが、実はフーリエ変換ではありません。
だから、（10）式からFFTを直接的に求めることは出来ません。

厳密に言えば、FFTは「離散的なフーリエ級数展開（DFS）の係数を高速に求める手法」です。

なんのこっちゃ？とお思いでしょうね。フーリエ級数展開というのは、高調波による時間領域での展開式です。

あらゆる周期的な関数は、必ず正弦波の加算合成で表される、と言う事をご存知ですか？いわゆる高調波というものです。

例えば1kHzの周期波形（矩形波など）の高調波は２ｋ、３ｋ、・・nkという風に1kの整数倍ですね。
つまり、方形波だろうと、のこぎり波だろうと、1kHz の周期波形は、1kHz の整数倍の正弦波で合成できるのです。

証明もできるんですが、多分、直感的に理解できる所じゃないでしょうか。（私も書くのが面倒だし ^^;）

というのは、1kHzの周期波形に、それより低い周波数成分、例えば500Hzがあったとしたら、絶対に周期は１kHzより長く、500Hzになっちゃうでしょう？

1.5kHzの成分が含まれれば、1kHzの周期（1/1k）でみれば、1.5kHzの4/3が含まれることになりますよね。
ということは、割り切れてないわけですから、最早その周期じゃないって事です。（わかりにくいかな？^^;）

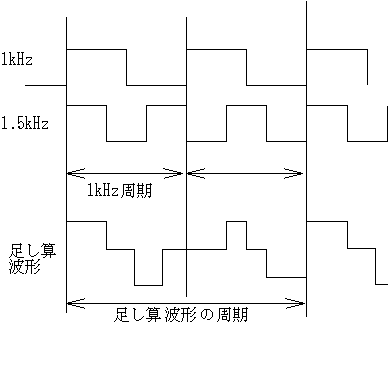
このことを図にしたのが上の絵です。解りやすいように矩形波で表しましたが、正弦波でも性質は変わりません。
図のように、1kHzの周期信号と1.5kHz周期信号の足し算波形は、最初の周期と次の周期が違ってしまいます。
周期波形ってものは同じものがずっと続いているもの、一周期を取り出せば全部繰り返し同じであるものを指すわけで、つまり足し算波形の一周期は、この1kHzの周期じゃないんです。

この例では足し算波形の周期は、1kHzよりも長く、倍の長さの500Hzになります。
て事は、これは1kHzじゃなくて500Hzの周期波形って事ですね。
1kHzも1.5kHzも500Hzの整数倍なので、やっぱり500Hzの整数倍の高調波しか含まないって事になります。

フーリエ級数展開は、このことを数学的、定量的に表したものです。そのディジタル版が離散フーリエ級数展開（DFS）です。
実際の計算にDFS の定義式は役に立たないので、ここでは取り上げません。FFT は結局のところ、プログラムコードになって初めて役に立ちます。

ここで、ある任意の波形のスペクトル解析を考える時、「窓」という概念を持ち込みます。(下図)

この窓の中の部分だけが、過去から未来まで、永遠に繰り返す周期波形であると仮定するのです。
周期波形ですから、フーリエ級数に展開できます。つまり、高調波で解析できるので、ＤＦＳが使える訳です。

そうすると、その窓の周期（＝サンプリング周期×ポイント数）で分解される周波数精度で、スペクトルが計算できる訳です。
例えば、サンプリング周期が 10μsec (=1/100kHz) で2048ポイントの FFT なら、1/(2048･10μ)＝48.83Hzです。
これが周波数分解能です。これは、48.83Hzの高調波成分を求めることと同じです。だから、DFS と FFT は本質的に同じです。

言い替えると、窓の大きさは、サンプリング周期×ポイント数ですから、これより長い周期の信号は計算できません。
だから、この窓の周期（＝1/48.83Hz）が分解能です。

但し、窓のはじっこの部分でつながらなくなってしまうので、図の点線のように、中心に向けて徐々に大きくなる関数で重み付けをします。
これを「窓関数」といいます。普通に使われるものに、矩形窓、ハミング窓、ハニング窓、ブラックマン-ハリス窓等があります。
歪みなどの解析には、ハニングが良く使われます。インパルス等の過渡応答が見たいなら矩形窓です。

これを高速演算する手法がFFTです。どうやったらコンピュータで計算するのに都合が良いかを考えるのです。
回転因子という概念で説明されますが、書き出すときりがない部分なので、この辺で止めておきます。

どうも、時々勘違いする人が居る様なので、追記します。
離散信号のフーリエ変換、即ち (10)式は、通常は周波数軸で見た時に連続な関数です。
これに対して、FFT は不連続な関数です。連続な関数の全て点を計算で求めるのは勿論不可能です。
時間軸の打ち切り--即ち窓の概念--と、周波数軸での離散化--即ち不連続な関数と捉える--、という作業を行って、初めてコンピュータでの計算が可能となります。無限の点の乗加算も、無限の周波数軸上の点の計算も出来ないのは明らかなのですから。

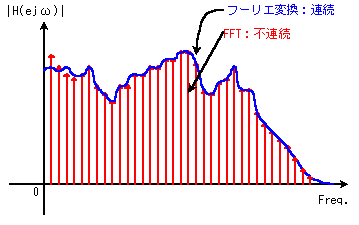
つまり、図に示す様に、いわば FFT は周波数領域でサンプリングした状態です。
信号の成分に対してポイント数が不十分だと、一般に低域で誤差が大きくなりがちです。

なお、文献の一部には、DFT（離散的フーリエ変換）という言葉が、 (10)式を用いて書いてある場合があります。多分、DFS と DFT を区別する目的でそういう書き方をしているのだと思いますが、これは極めて厳密に言うならば誤りです。
DFTと FFT は本質的に同じで、周波数軸で不連続な関数を表します。つまり、DFT はフーリエ級数展開から誘導できます。そうする事で、周波数でも時間でも離散的になります。

私が学生の頃には、「本には、常に正しい答えが書いてあるとは思うな！」と叩き込まれました。
これは即ち、「自分で良く考えてから、答えを出せ」と言うことです。実際に、私は明らかな誤りを見つけた事もあります。
何が正しいのか、自分で良く考えて下さい。

私が何言ってるか解らない人、ヒッポファミリークラブの「フーリエの冒険」がおすすめです。それでも解らなければ、中学校の教科書をもう一度勉強しましょう！