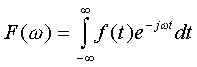 (1)
(1)
フーリエ変換とは、ある任意の時間信号を周波数領域で表したものです。
フーリエ変換論をまくしたててやろうかとも思ったんですが、多分誰も読まないので、端折って、回路に使う解説とします。
数学的には、フーリエ変換はアダマール変換等と同じ仲間で、直交変換に属します。
フーリエ変換はフーリエによってつくられ、シュヴァルツによって開花しました。
ここでは、数学的厳密さは完全に無視して、「物理的イメージ」 フーリエ変換でいきたいとおもいます。
もし、厳密な意味を知りたければシュヴァルツの本でも読んで下さい*。
「超関数論」(1951)。 日本語訳:岩村他訳「超関数の理論」(岩波書店)
数学的厳密さを無視しているのは、厳密にすればするほど、既に解っている人にしか解らないシロモノになるからです。
例えば、厳密に表現したら、
「フーリエ変換の定義 (1)式が存在するためにはコーシーの意味で主値を持つことが仮定されている、何故なら・・・(延々と証明続く)」
なんて事になります。終いには何が目的で何をやっていたのか、忘れてしまいます。
(私の見るところ、実は物理学や電子工学を学んだ人でも、その物理イメージを持ってる人はごく少数です。その理由は、上述のような訳のわからん数学を授業でやる大学教授に問題があると見ています。)
正しいことが必要なことであるとは限りません。共産党的見解には、興味がない人の方が多いのです。
*私は、Laurent Schwartz と Hermann Amandus Schwarz を勘違いしていました。
ご指摘を幾重にも感謝します。m(__)m > Special Thanks to Mr.Hunt.
最初に書いたように、フーリエ変換とは、ある任意の時間信号が周波数領域でどうなるかを式で表したものです。
フーリエ変換の定義式は、ある連続な関数 f(t)において、角周波数をω=2πf とする時、
です。逆変換もありますが、ここでは触れません。j は虚数単位です(j2=-1)。
電気関係では、電流の i と区別するために、虚数単位は j で表します。
また、通常この種の計算は、アナログであれディジタルであれ、角周波数ω=2πfで表しますから、これに慣れて下さい。
この式が、周波数と時間関数との関係を表しています。つまり、両者は独立したものでは無いのです。
立ち上がりの速い信号には高周波が含まれているし、ゆっくり変化した信号には低周波が含まれる、という事です。
ここで重要な関数が、δ関数(デルタ関数≒インパルス)です。インパルスは、時間 t=0 に於いてのみ値を持つので、その値を1とすると、
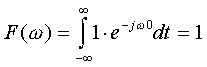 (2)
(2)
であり、つまり全ての周波数で一様に値1を持ちます。
もっとフランクに表現すれば振幅も位相も、全周波数帯域において周波数特性がフラットですよ、と言っているんです。
この計算は純粋数学的には誤った解釈(δ関数は本来‘超関数’であり、上式は成り立たない)ですが、オーディオにはこれで十分でしょう。
閑話休題、世の中には物凄く頭が悪い人がいて、これをゼロで割る事と同一視するという血の巡りが悪い方もいるようですが、高校数学レベルで判るレベルの間違いですので敢えて詳しくは触れません。しかしこういう人がいわゆる疑似科学に染まるのだ、と言うことです。
言い換えると、インパルス応答が解れば、それをフーリエ変換する事で複素周波数特性(つまり、振幅と位相)が解りますよ、と言う事です。
オーディオでは何故かこういう計測法にお目にかからないのは、私には不思議です。
それはともかく、純粋な正弦波をフーリエ変換したらどうなるでしょうか?
これは、直ぐに想像が付くことと思いますが、下の図の様になります。
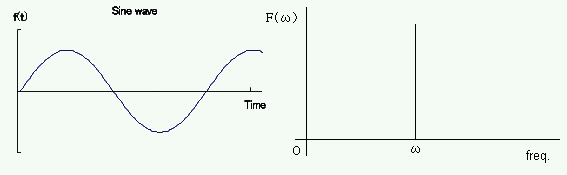
これを線スペクトルといいます。
周波数領域でどんな複雑な特性であっても、この線スペクトルに係数を掛けたものを無限に細かく見れば表現できる、というのは解りますよね。
つまり、図にすると
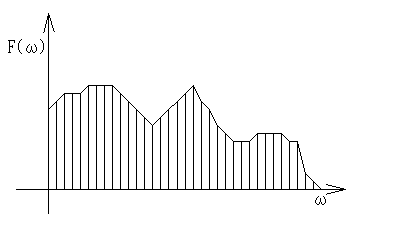 こんな感じです。
こんな感じです。
これが、式(1)が言っている事なんですよ。
何故 (1) 式がそうなるのか?
ここでいよいよ (1)式の物理的イメージを考えてみましょうか。
それには先ず、オイラーの公式
![]()
というものを知る必要があります。
(これの証明は、マクローリン展開してやれば出来るのですが、そのマクローリン展開の証明はかなり長くなるので割愛します。)
この式は、数学的には複素平面上での単位円ですが、物理的に言えば、複素領域での正弦波です。
だから、(1)式の積分の中身は正弦波と f(t)のかけ算です。
正弦波と f(t) をかけ算したものを、積分した式が(1)です。
積分ってのは面積を求めることですね。
ここで、直感的に解りやすいように、正弦波を矩形波図形で表すこととしましょう。
下図のような波形で ejωt が表現できるものと仮定して考えて下さい。
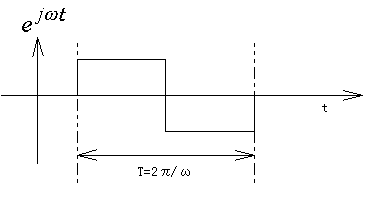
ここで、f(t) として下の図のような波形を考えます。
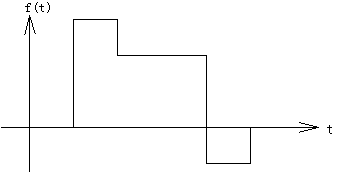
この f(t) と ejωt の積を、積分する事を考えるのです。これは式で表すと
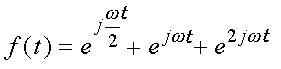 (3)
(3)
です。つまり3つの正弦波の合成です。
下の絵を見て下さい。
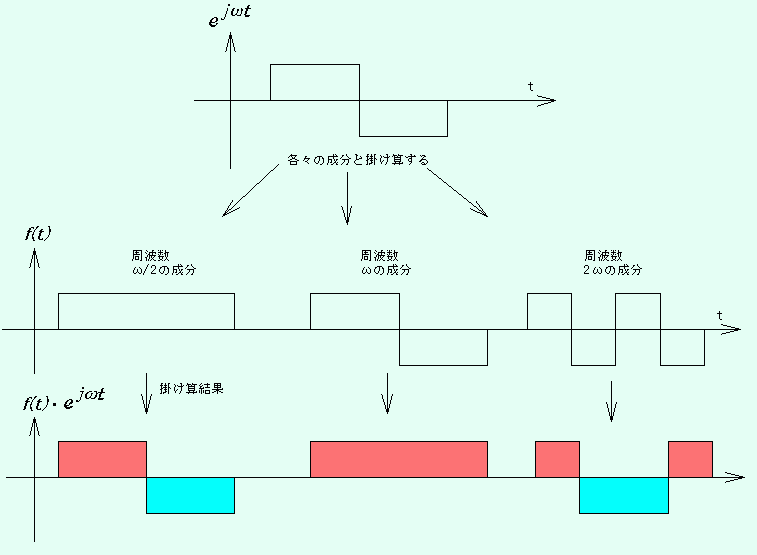
ωと同じ角周波数以外は、かけ算した結果の積分(=面積)が全部キャンセルされて、面積ゼロになることが解りますね。
(0を中心にして、赤で示した正の部分と、青で示した負の部分を加算した面積は、+と−が同じ面積なので相殺されて
0です。)
解りますね。つまり、任意の角周波数ωにおける値が求まるわけです。
だから、ω=ω/2 の時と、ω=2ωの時も同様にある値を持ちます。
だから、(3)式のフーリエ変換は
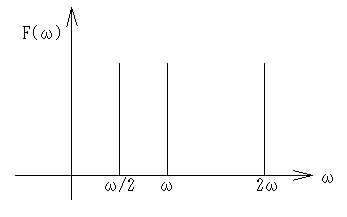
この様になるわけです。
解りやすいように矩形波で表しましたが、これは正弦波でも同じです。何でこんな事になるかというと、矩形波とサイン波は、同じ性質を持っているからです。それは、相異なる周波数では直交する(内積が零になる)ことです。
*これを言い替えると、AM変調して直流電圧を測るのと同じ事です。
周波数ωの正弦波と、 f(t)
のかけ算は、f(t)の周波数がωだけシフトします。これがAM変調です。
つまり(1)式は、ある角周波数ωでAM変調したものを、全時間領域で積分したものです。
ここで示した例は、周波数軸上では不連続な関数ですが、これは周波数軸で連続でも、またどんな複雑な関数でも成立します。
つまり、任意の関数について、任意の角周波数ωでの値が計算できますから、ωの関数として見れば、(1)式が成立する、というわけです。
何だか、(1)式と似ていますね。でも、本質的には違うんです。これは、数学的には微分演算子(後で説明します)の一種です。
物理的には、通常、「1入力・1出力で、線形、時不変なシステム」 の伝達関数(システム関数)を表現するのに使います。
鍵括弧の中身が重要な違いで、出力が自乗になるとか、整流器のラプラス変換なんてありません。
ここでは ±∞で示していますが、 0-∞(片側ラプラス変換)でも構いません。(フーリエ変換は原理的に±∞しか在りえません。)
更に重要な違いは、過渡的な現象に関しては(1)式は現せませんが、(3)式はそれを含んでいます。
これを数学的な言葉で言い換えると、
![]()
である、と言う事です。つまり上式の複素関数において、σ=0 の時がフーリエ変換であり、過渡的な現象を考慮しない、システムの周波数特性を現している訳です。
つまり、フーリエ変換は、無限に続く信号の全てを見たときの、周波数の分布ですが、ラプラス変換はより広い意味を持つことになります。従って、ラプラス変換はフーリエ変換の自然な拡張であると言えるのです。例えば、厳密に言えば正弦波のフーリエ変換ってのは無くても(エネルギーが無限なので。フーリエ級数展開は可能)、ラプラス変換は存在します。
面倒な理論に興味を持つ人は少数派でしょうから、使い方中心に説明しましょう。
ラプラス変換は最初に触れたように、微分演算子の仲間(数学的厳密さは無視しています)です。
微分演算子というのは、連立微分方程式を簡単に解くための手法で、微分を s、積分を 1/s と置く事で、大袈裟に言えば中学校で学んだ連立一次方程式と同じ要領で解けますよ、と言う 誠にもって ありがたいやり方です。
これを電気回路に当てはめます。世に積分回路と言われる回路を例に挙げましょう。

Cに流れる電流と電圧の関係は
![]()
ですね。積分を 1/s と置けば上の回路は下図のように書き換えられます。
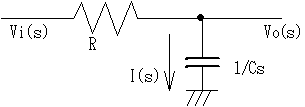
C は(4)式から、1/Cs になっている事に注意して下さい。電流 i と電圧 v は、時間関数から s平面(ラプラス平面)に写像したので大文字で表現します。
コンデンサーのインピーダンスが、s平面で 1/Cs (インダクタンスはLSです) であるので、オームの法則から
Vo(s)=I(s)・1/Cs 、Vi(s)=I(s)・(R+1/Cs)
ですから、これを連立させて、
を得ます。このH(s)がこのシステムの伝達関数です。
つまり、入力 Vi と出力 Vo の比です。入出力の比がシステムの伝達関数である、というのは直感的に理解できるんじゃないでしょうか。
s=jω を代入すれば、それはフーリエ変換ですから、複素周波数特性が得られる訳です。
これを jω 解析と言います。
(5)式を 逆ラプラス変換したものが、システムのインパルス応答になります。つまり、過渡応答が解る訳です。
逆変換の公式もありますが、実際に計算する時は(5)式を部分分数に展開して、ラプラス逆変換表より求めます。
伝達関数にはもう一つ重要な性質があります。
それは、今、二つのシステムがそれぞれ伝達関数H1(s)、H1(s)を有する時、H1(s)とH2(s)を直列に接続した伝達関数は各伝達関数の積になることです。これは直感的に理解できるでしょう。即ち、
H(s) = H1(s)H2(s) ---(6)
しかし、ここで注意すべきは、(5)式の伝達関数で表されるシステムをそのまま直列に接続した場合には(6)式にはならない事です。何故なら、この回路の出力インピーダンスは零ではないからです。
最初にVi(s)=I(s)・(R+1/Cs)として解いています。つまり、この式は信号源が純粋な電圧源と仮定しています。
言い替えると、もしも信号源がインピーダンス Z を有するなら、
Vi(s)=I(s)・(Z+R+1/Cs) です。
従って、最初に示した積分回路への入力信号源がインピーダンスZを有する時には、この式に従って伝達関数 H(s)を求めなければなりません。即ち、信号源インピーダンスも回路の一部なのです。
従って、もしも(5)式の従属接続関数が要りようなら、間にバッファー回路(インピーダンス変換)が必要です。
オーディオでは、しばしばスピーカーのネットワークなどでこの辺りの事を誤解した設計が目に付きます。
例えば、LPFとHPFをそのまま接続すれば、一応BPFの格好にはなりますが、当然計算上のFcは変わってしまいます。
但し、十分に両者のFcが離れていれば、概ねFcはそのまま使えますが、その場合にもスピーカーのインピーダンスの変化があるので、インピーダンス補正は必須です。
因みに、時間領域で従属接続を計算する場合には、バッファーがあっても、各々の時間関数の積にはなりません。
時間領域なら畳み込み積分になりますから、実際問題として計算は困難です。
この事があるから、伝達関数による計算は威力があるのです。
また、一入力一出力ではない場合とか時変回路等では、最初に述べたように伝達関数で表すことが出来ません。
その場合、マトリックスで計算するのですが、それでもここに述べた伝達関数論が基本となることは当然であります。
過度応答
ラプラス逆変換を、実際の回路で何に使うか、というと、例えば上の積分回路で、出力にトランジスタとリレーを設けて電源のパワーON時にミュートする事を考えてみましょう。
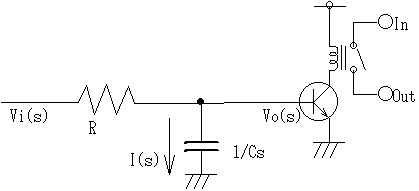
Viを電源に接続します。この時、トランジスタが何時ONするか?という問題を考えてみます。
簡単のため、ベース電流は無視します。
入力の電源が1Vで、ステップ関数的に立ち上がると仮定しましょう。すると、入力の関数は、時間的には
時間 t が−∞から0の区間 → vi(t)= 0V、 0から+∞の区間 → vi(t)=1V
ですから、これを(3)式に当てはめると、Vi(s)=1/s
になります。(もし、0V→5V に変化する関数なら 5/s です。)
(6)式から、入力信号があるラプラス変換式で表される場合には、入力信号とシステムとの積になります。
つまり、(5)式で得られた伝達関数に、Vi(s)=1/s を乗じて、ラプラス逆変換してやれば、その時間関数
vo(t) が得られます。
![]()
これが得られる関数です。ステップ応答、またはインディシャル応答と言います。
vo(t) がトランジスタをONさせる電圧、つまり0.6V+α になる時間を求めれば良い訳です。(Siトランジスタで常温の場合です。)
この例では、時定数RC=1の時、t≒1[sec] になります。
これぐらいの式なら、別に元の微分方程式から直接求めることだって出来なくは無いんですが、たとえば上の回路にRと直列にLが入ったとしたら・・・
もはや直接的な方法は困難です。次数の高いものほど、伝達関数とラプラス変換のありがたみが出てきます。
Next Page