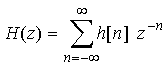
です。
ディジタルシステムとその回路について述べる前に、先ず知っておかなければならないのが「Z変換」です。
定義式は
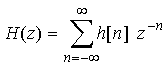
です。
FFTのページで触れた離散時間フーリエ変換と良く似ていますね。そう、z = ejωとする事で離散時間でのフーリエ変換の式になります。
nT→ n としていますが、一般にディジタル信号の計算にサンプリング周期 T は無関係です。コンピュータで計算するのですから、入力信号は単なる数列として扱えるからです。
但し、サンプリングレート変換の場合にはこの限りではありませんが、これとても T = mT' となるだけで、T の絶対値が問題になる訳では無く、問題になるのは m の方です。(オーディオでは、CD等で使われるオーバーサンプリング・ディジタルフィルタとして知られています。)
明らかにz = ejωとする時、離散信号のフーリエ変換の定義式に一致します。
つまり、システム関数から周波数特性その他を、アナログの場合と同様に計算できます。即ち、H(z)・H(z-1) に対してz = ejωを代入すれば良いのです。注意する点は、z-1 は z の複素共役である事です。
アナログで周波数特性を求める際に H(s)・H(-s)としたのは、S=jωを代入すると H(s) と H(-s) が複素共役になるからです。
z = ejωTの持つ意味
ディジタルシステムにとっての z =ejωT 意味を明確にしましょう。
e-jωT F(ω) =e-jωT∫f(t) e-jωtdt =∫f(t)e-jω(T + t)dt
ここで、 t -T = x と置くと
= ∫e-jω(T + x)dx
= ∫f(t-T)dt
となります。即ち、これは元の信号 f (t) を、サンプリング周期
T だけ遅延させた信号 f (t-T) のフーリエ変換である事を示しています。
従って、サンプリング周期によって遅延するメモリーがある時、それは式の上では
e-jωT との掛け算で表される、という事です。
言い換えると、1サンプリング周期のメモリだけのシステム
f(n) --->T ---> f(n-1)
は、システム関数 H(z) = z-1 である、という事です。
解らない? OK、解らなくても、後は理解できます。ともかく、 z-1
が1サンプリング周期の遅延であることだけ、頭に入れておいて下さい。それを証明しただけです。
それとも解った?なお宜しい。後の理解が容易になります。
微分する、という事は即ち接線方程式を求める事に他なりません。しかし、サンプリングされた関数
f(n) は不連続な関数です。
アナログ的に考えた場合、不連続なものの接線は無限にあります。でも、ディジタル的には“そこにしか値が無い"ので、連続的に考えること自体が無意味です。つながった数列と考えるべきなのです。
そこで、一つ前の値との差をとる事で接線の傾きと考えると、それは図-1a のようになります。
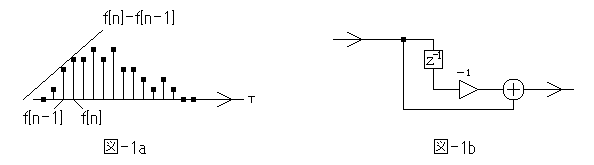
これがディジタルシステムでの微分回路に相当します。これを、一次後退差分と言います。
アナログ的な意味での微分というか、sinx/x で補間した関数(即ちサンプリングする前のアナログ波形)への微分を考える場合には、より高次の差分値をとればできます。
簡単には、テーラー級数展開の n 回微分を n 回の差分値で表せば、それらしい値になるでしょう。
積分するのは面積を求める事です。サンプリングされた信号では、そのサンプリング点にしか値を持ちません。間の値は存在しませんから、要するに、サンプリング点の値を全部足してしまえばそれが面積になります。
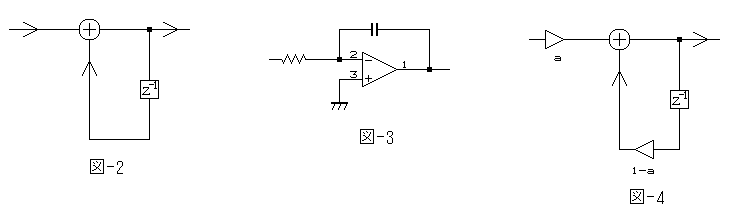
上図-2 に示す回路にすれば、一つ前の値と加算された値がまたメモリーに蓄えられ、さらに次の値と加算され・・・という具合にどんどん蓄積されます。これが積分です。
でも、図-2 の回路は実は上手く動作しません。何故なら、全ての入力信号が蓄積されるので、微少なDCでも簡単にオーバーフローしてしまうからです。これは本質的にはアナログ積分器を上図-3 で構成した場合と同じで、実用にはなりません。
図-4 の回路なら動作します。この場合は、係数の和が 1 なので、直流増幅率は 1 です。
図-2~4 は、全て一次のフィルタです。
FIR と IIR
ディジタルフィルタには FIR(Finite Impulse Responce:有限インパルス応答)と IIR(Infinite Impulse Responce:無限インパルス応答)があります。
アナログでは普通は有限時間応答はありません。但し SAW(Surface Accurstic
Wave:弾性表面波フィルタ)は設計理論的には FIR があります。
しかしながら、物理的に厳密に見るなら時間応答と帯域幅にはΔt・Δω≧1/2
という関係(不確定性原理)が成立するので、厳密な意味で言えばアナログの
FIR というのは存在し得ません。
ディジタルの場合は、周波数領域が-π~+πで有界なので、完全なFIRでも矛盾しないのです。
IIRというのは、上の図-4、図-5等がそれです。要するに、演算語調が無限大ならインパルス応答が収束するのは無限遠点になります。
IIRフィルタの伝達関数設計を理解するには、先ずはアナログフィルタの伝達関数設計を理解している必要があります。
このページをお読みの方々にそれを要求するのは、ちょっと酷というものでしょうから、割愛します。
FIRは、普通はトランスバーサルフィルタで構成します。「普通は」と言ったのは、ディジタルフィルタには、帰還の掛かったFIRも存在し得るからです。
FIR トランスバーサルフィルタの一般的な構成を下図に示します。
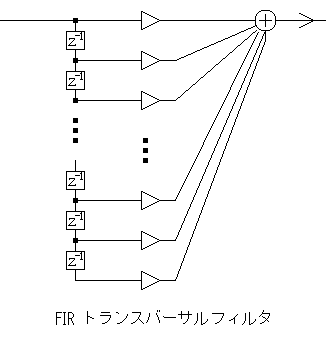
図1-bで示した微分器は、遅延器が一つで、係数が 1 と -1 の場合と考える事が出来ます。
この構成であれば、完全直線位相が実現できます。
IIRでは直線位相は実現できません。
何故なら、完全直線位相である事と、そのインパルス応答特性が時間対称である事は等価だからです。
明らかに、無限に続くインパルスを時間対称にすることは不可能です。
各々の係数(図中の三角形で示した乗算器)は、インパルス応答そのものです。
インパルス応答をフーリエ変換するとその周波数特性が得られることは既にお話ししました。
インパルス(δ関数)のスペクトルが完全にフラットであることもお話ししました。
このフィルタにインパルスを入力すれば、明らかに各係数が順番に出力に出てきます。
だから、フィルタ係数は、必要な任意の周波数特性の逆フーリエ変換(I-FFT)です。
よって、この形のフィルタの伝達関数は、最初に述べた Z変換の定義式そのものになります。
この形のフィルタの伝達関数設計で、任意の次数で最大減衰を与える係数は、初等的に求めることが出来ません。
Remez Exchange アルゴリズムと呼ばれる、漸化的な計算手法によります。明らかに本HPの範囲を超えるので、説明は割愛します。
オーバーサンプリング・ディジタルフィルタ (インターポーレータ)
CD等で用いられるオーバーサンプリング・ディジタルフィルタの設計手法について述べます。
実はオーバーサンプリング・ディジタルフィルタという名称は正しくありません。正しくはインターポーレーション(補間)フィルタと言います。
オーバーサンプリングとは、本来の意味では信号の持つ帯域幅よりも広い帯域の信号をA/D変換する事、つまり遥かに高い周波数でサンプリングする事です。これを間引きするフィルタをデシメーションフィルタと言いますが、正しくはこれがオーバーサンプリング・フィルタです。
これらのサンプリング周波数が変化するフィルタを総称して、マルチレートフィルタと呼びます。
どういう訳だか、オーディオ業界は勝手な言葉を作っては業界用語にしてしまう傾向があるので、オーディオを知らない人には話しが通じなくなってしまいます。
他にも例えば、‘DSP’と言えば、本来は‘Digital Signal Processor/Processing’を指すのですが、何故かオーディオでは‘Digital Suround Processor’だったりします。本HPでもDSPと書いてある部分がありますが、私は本来の意味(ディジタル信号処理ないし信号処理プロセッサ)で使っているので、誤解のなきようお願いします。
閑話休題、前置きが長くなりました。サンプリング周波数を整数倍に上げるための原理を説明します。
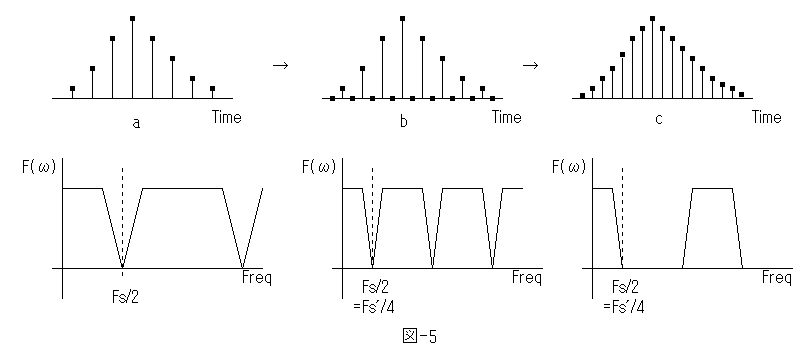
入力ディジタル信号が a とすると、これに零値を補間したのが b です。このようにしても,アナログのドメインで見ればスペクトルは変化しませんが、ディジタルのドメインで見れば、サンプリング周波数との関係が Fs/2→Fs'/4 のように変わります。
数学的な証明も出来るんですが、恐らく直感的に理解できると思います。
にも関わらず、ディジタルのドメインでみれば明らかにサンプリング周波数(Fs)が2倍になっています。
ディジタルのドメインでは周波数ωはπ/2(=Fs/2)で上に有界ですから、a の信号を元のスペクトルを保ったままフィルタリングする事は出来ません。 b の様にする事で、初めてサンプリング周波数が変化し、元の Fs/2 より高い周波数をフィルタリングできるのです。
これをフィルタリングしたのが c という訳です。だから各々の時間は系のスペクトルが図に示すようになるのです。
ここで注意すべきは、フィルタに入力されるデータの二個に一個は零であることです。(零を挿入したのですから当たり前です。)
但し、係数を一回計算する毎に(上述の例で言えば1/Fs'毎に)偶数番目の係数と奇数番目の係数を交互に用いることになります。
ここで、さらに条件があります。元の信号の各点は、正しい入力信号ですから、そのまま保たなければなりません。
これを防ぐ為には、トランスバーサルフィルタは偶数次であり、真ん中のフィルタ係数(例えば50次であれば25番目)は必ず1です。
そして、周りの係数は2個に一個は零にします。
符号間干渉を考慮した、完全直線位相ローパスフィルタのインパルス応答(即ち係数)を下図に示します。
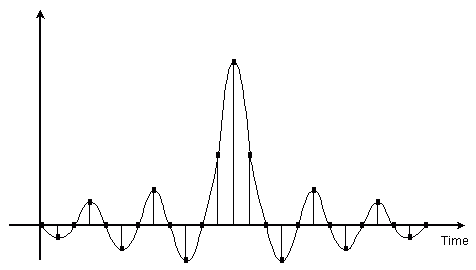
図-6 符号間干渉を考慮したフィルタのインパルス応答の例
図に示すように中心の値(係数1)に対して、他のデータのあるところは係数が零になるので、元の値は変化しません。
だから、ポリフェーズフィルタで半分になった計算量は、さらに半減できます。
実際問題として、乗算器や加算器のハードウエア規模は大きいので、沢山装備するわけにはいきません。
従って、時分割多重化処理によって計算されます。IC内部では、マイクロコードと呼ばれるソフト的な処理で動作しています。
(マイクロコードとは、CPUの機械語より低級な言語。CPUも、機械語を最終的なハードで処理するために、内部ではマイクロコードが動いています。こういうやつをファームウエアといいます。)
だから、計算量を削減することは、次数を減らすのと同じ効果があります。
最近は、CDプレーヤーをはじめとするほとんどのディジタルオーディオ機器のD/A変換器にΔΣ変調方式を用いています。
俗に言う‘1bit DAC’(これもオーディオ専用語)です。
これは、上述の手法(Rabinerの方法)で補間されたデータに対して、ノイズシェーピングと呼ばれる手法でより高い周波数に量子化雑音を追いやる事で、低周波の分解能を上げるやり方です。
これは、フィルタリングとは意味が違います。
何故なら、補間によるフィルタリングは明らかにエイリアシングノイズのパワー(折り返し雑音の電力スペクトル密度)を小さくしているのですが、ノイズシェーピングは量子化ノイズの密集している周波数を変えるだけで、トータルのノイズパワーは同じだからです。
ノイズシェーピングの原理は負帰還そのものです。ディジタル領域での負帰還なのです。
できるだけ計算式による説明を減らして、解りやすく説明したつもりですが、未だ解りにくいようであればメールでお願いします。