The maximum power of the output transformer
and its high frequency response

Normally the output transformer has a limitation value of output power.
Generally speaking, it is written like as "50W at 30Hz".
Here I explain the meaning of this spec and also a high frequency response of the transformer.

The maximum output power should be defined by the low frequency.
At first, you have to understand this point.

The exciting current is also related, and it should flow for the primary inductance of the transformer. If no exciting current, transformer does not work.
In equivalent circuit, the primary inductance is in parallel to the primary winding.

So, if the inductance value is smaller, of cause lower frequency response will be worse. This value defined the lower frequency response of the transformer. The maximum power of the transformer is strongly related to the inductance, but is not just the same. It is "magnetic field saturation".

I have used "Amplimo" transformer and its maximum power is defined by 20Hz (-3dB start point), so its allowable maximum voltage of primary winding is larger than typical Japanese transformers in realistic.
I'd like to explain this point.

As I wrote above, the maximum output power of the transformer is defined by the magnetic field saturation, which means the saturated magnetic flux density of the core.

What is the magnetic flux? and why core is magnetized?
The physical reason is the "spin" of the electron. (but please notice, the spin of the quantum physics is different from classic image.)

The core of the transformer is the ferromagnetic substance, which makes a magnetic domain. The magnetic domain is similar to the very small magnet in the big magnet.

If there is no magnetic field, all magnetic domain are different direction.

Then, why there are magnetic domains in the ferromagnetic substance?

Normally, an electron makes a "pair" of different spin around the atomic nucleus. If all electrons make pairs, no magnetic fields can be found.
However, for example, ferrous metal (iron) has a irregular orbit, 5 left spin and one right spin, so in this case we can see the magnetic field to the iron.

Atoms of the iron are connected by the covalent bond, but in above case, the covalent bond is not found because of Pauli's law.
In stead of the connection of the outermost shell, atoms are existing "in parallel" but the same direction of the spin, if its potential energy is lower.

(This is also the reason of the hysteresis, but if you want to know more details please read the textbook of Physics.)

Therefore, if all the magnetic domains become the same direction by the very strong electric field, we cannot get more strong magnetic field.
This is just the magnetic saturation.

So, the saturated magnetic flux density is individual value of the core, which is defined by the core material and the size, especially its perpendicular area to electric field.
We generally call it "B_max", and now let's consider the relationship between B_max and the voltages for primary winding.

Maxwell equations

    …eq.1

Here I calculate the surface integral for the magnetic field perpendicular to the electric current (in other word, the direction of the area of core)

    …eq.2
Here, n is the unit normal vector.

According to the Stokes' theorem, the left side of equation is

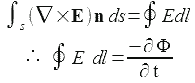    …eq.3

The left side of the equation is the contour integral of the electric field surface of C loop, which means the voltage difference of one turn for any area in loop C.
The right side is the time differential of the flux Φ which penetrates through the plane S caused by the loop C.

In other words, The voltage potential appears in loop C to demagnetize the time differential of flux B.

The left side is the voltage difference between the two terminal of the coil. So the voltage for one turn of the coil is 1/n times for each winding if n turns.
Therefore,

    …eq.4
This equation is called Faraday's Law.(Although sometimes eq.1 is also called so.)

Here differentiate the both side of above equation, then,

    …eq.5
Here, the initial value is zero as a boundary condition.
If the voltage of primary winding is the sinusoidal wave,

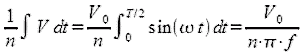    …eq.6
Here, V = V0·sinωt, ω = 2πf

Therefore we can get directly,

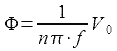    …eq.7

The magnetic flux density can be gotten that total flux divided by the area of the core, so,

   …eq.8
Here, B is the flux density, S is the area of core, which is the orthogonal part to the line of magnetic force.

Therefore, the magnetic flux density can be written,

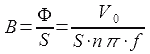    …eq.9

So, we can know the flux density is proportional to the input voltage, and is inverse propotion to the frequency.

Here we can know the very important point. If the same core is employed, the more number of primary winding turn brings higher maximum input saturation voltage.

So, in other words, the maximum output power of the output transformer means that the saturation input voltage V₀ at the specified frequency, which brings the maximum flux density of the core.

So the designer of the transformer considers the maximum power from the sectional area S and turns n.
Therefore, if the transformer maximum power spec was defined by lower frequency, that transformer allows more power than others.

Additionally, we can know that if we connect the lower impedance load than defined by the transformer spec, the primary voltage will be lower if the same power, so the flux density will not be saturated.
Therefore, if we connected 6 ohm speaker to this transformer, we can obtain more than 100W if output tube allows.

By the way, a troid is not always better than others. For example, the linearity of the inductance to the current is inferior to a solenoid.

As far as I heard, the leakage flux of the troidal transformer is very small at low power, but it is larger than EI close to the maximum power, and this leakage flux comes from the edge of the winding.

Transfer function at high frequency

Well, I talked about the allowable maximum power above, on the other hand we should know the higher frequency response.

This is concerned to many many kinds of characteristics ;)

These two are the main reasons of the high frequency limit, but profusely there are other reasons like as

• 3. The skin effect of the wire causes the high frequency resistance.
• 4. The proximity effect of the wire also enlarges the high frequency resistance.
• 5. The core loss increases due to the eddy current at high frequency. (Please notice, the eddy current of inside the wire conductor is different from this.)
• 6. The hysteresis loss of the core also.

The hysteresis loop of the core depends on the magnetize characteristics of its material.

The core is normally made from a steel sheet, or sometimes cold rolled oriented Si-steel sheet may be used for expensive one. The electrical resistance of the steel is low, so it causes the eddy current loss, however the thin sheet core material decreases this loss.

Therefore, at higher frequency, the core made from thin sheet is superior to thick one.

As far as I heard, if the core is constructed by the very thin core, the characteristic is close to the Fe-amorphous core. (Although amorphous is also very thin sheet, a few micro-meters.)
It might be truth, because the circumference of one atom of amorphous will be the same as a crystal, so it may be natural if very thin crystal sheet can be made.

And here, we can have an illusion that the nanocrystal core (like as Finemet) characteristic is understandable ;)

6. The hysteresis loss is proportional to the frequency. (I think this is easy to understand because the hysteresis loop was crossed by that frequency.), but next one "5. Eddy current" is proportional to the square of the frequency.
So, the edgewise winding with ribbon wire is good solution to decrease high frequency loss.

The leakage inductance and the distributed capacitance are the reactance, so they do not become power loss. However, AC resistance by the skin effect and the proximity effect is the loss as they are the resistor, and of cause core loss also, so they become a heat.

Generally speaking, the ferromagnetic material shows strong temperature-dependence, precisely its initial permeability shows an exit point at the temperature where the k1 becomes zero, so too high frequency input may cause miserable result.

By the way, my calculation for the stability does not include above 3 to 5, therefore the high frequency transfer function is calculated with the 2nd order.
I think above 3-5 losses are resistive, so for the stability of the feed back point of view, they may be welcome (probably ;).

In the thesis of Mr. van der Veen who design this transformer, the relationship of characteristics and parameters is written. He uses only above leakage inductance and distributed capacitance, but the transfer function changes with power tube output impedance, and its resistive part will be changed by the output power dynamically.

In my design, the transformer driving impedance will be almost defined by the local feed back, therefore it brings not only an easier mathematical analysis but also an advantage of the feedback stability.

Return to Japanese

Return to English