図 1.
折り返し雑音というのは、ディジタルドメインとアナログドメインとの変換において主に問題になる概念です。
ですから、D/A や A/D する場合のフィルタと、切っても切れない関係にあります。
これについて、少しお話します。
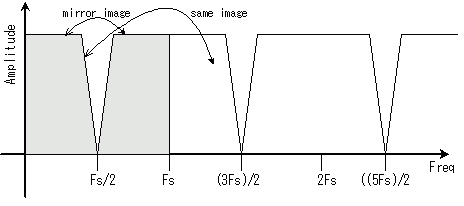
まず、フィルタの無い場合(ディジタルフィルタを含む)には、ディジタル信号をアナログに変換すると、下図 1. のようなスペクトルになります。

これは、離散信号のフーリエ変換が
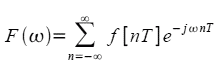
で表される事からも、容易に理解できます。
このスペクトルは、同じものが(理論的には永遠に)繰り返しています。
Fs/2〜Fsは、0〜Fs/2と鏡像対象です。これが折り返し雑音です。
ADCの場合には、もしも Fs/2 よりも高い成分が含まれると、0〜Fs/2 へと内側に“折り返して”きます。
だから折り返し雑音というのですが。
ディジタルフィルタがある場合には、例えば8倍に補間すれば、8Fsで繰り返しますが、Fs/2〜4Fsがフィルタで消されることになります(4Fs〜(15Fs)/2 も鏡像で消えていますが)。
これをフィルタリングすることで、アナログ波形を得ます。
世に言うサンプリング定理(標本化定理)というのは、畢竟、この 0〜Fs/2 のスペクトルの保存を指します。
『あるアナログ領域での信号を標本化する場合、その信号に含まれる成分が“Fs/2 以上の成分を含まない時に”標本値から元の信号が完全に再生される』と、書かれています。
逆に言って、Fs/2 以上の成分を、標本化する前にもD/Aした後にも含んでいたら、元の信号を再生する事はできません。
言い換えると、図 2. に示すように、Fs/2 以上の成分を急峻なフィルタで遮断してやる事と、時間領域で( sinξ/ξ の形のいわゆる sinc関数で)標本値の間を完全に補間(内挿)することは同値である、ということです。
ですから、例えばサンプリング周波数を高くしたから 20kHz の分解能が変わる、なんて事は無いという事です。
ADC に関して言えば、折り返し雑音が生じればこの限りではないのは当然ですし、現実には無限大の減衰を持つフィルタも存在しないので、可聴帯域端でほんの僅かに変わると言えばそうかも知れませんが、それが問題になるかどうかと言えば、疑問です。
普通は周囲の環境雑音やマイク自身の雑音とかの方が遥かに大きいからです。
16bit の分解能って、アナログで実現するのは、そう簡単では無いのですよ。
こっちのページではディジタル領域での補間(いわゆるオーバーサンプリングディジタルフィルタ)について書きましたが、これは、アナログ領域でのそれが連続関数で補間するのに対して、ディジタル領域では離散関数で補間する事に相当するわけです。
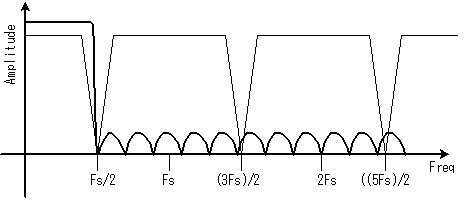
だから、基本的にスペクトルの保存という観点で言えば、できるだけ急峻なほうが良いのです。
一方、オーディオでは、周波数領域でのスペクトルの保存とは違った方式があります。どちらかといえば、比較的高価なものに多いです。日本ではレガートリンクとかフルエンシーとか、海外ではまた別の名前が付いたものもありますけど、まあ微妙な特性の違いですね。
この種がどうなっているのかと言えば、早い話が、下図 3.のように緩やかなフィルタで遮断しています。俗に言う "Slow roll off" ですね。
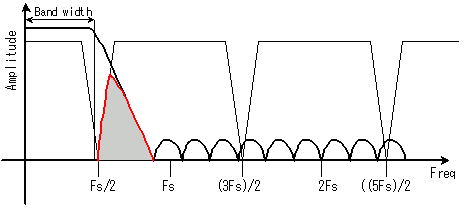
この図で言えば、赤で囲った部分が残る事になります。無論、信号成分とは相関がありますが、しかし「ひっくり返った」スペクトルですから、必ずしもこれが有効という保証はありません。
ここで、帯域幅について勘違いがあるようなので簡単に触れておきます。
帯域幅と言うのは、普通は半値幅(パワーが半分になる帯域)を指します。従って、この場合でも、帯域幅に差はありません。
図 3.にこの様子を示します。Bandwidth と書いた部分が帯域幅です。
つまるところは、それより上の帯域は一定レベル以下なら、「帯域幅」という意味での計算や計測に対しては無関係である、と言う事です。
(無論、聴感はまた別の問題ですよ。帯域幅という概念を説明してるだけですから、誤解無きようにw)
これが時間領域でどうなるかと言いますと、周波数領域で急峻なフィルタほど、時間領域では“暴れた”特性になります。
例えば、インパルス(物理で言うディラック デルタ)は「全く帯域制限されていない」状態です。つまり、帯域制限されていない状態では、時間領域で振動しないのです。
だからディジタルドメインの周波数領域で帯域制限すれば、時間領域ではこんな特性になります。
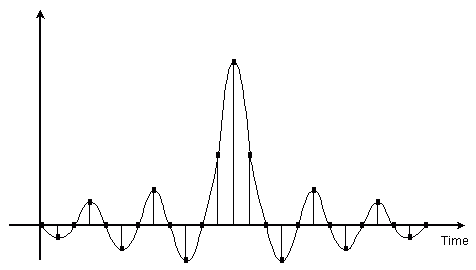
周波数領域で急峻なフィルタほど、時間領域での振動は長くなります。
インパルスそのものを畳み込んでも何も変わらない(帯域制限されない)のは明らかですから、帯域制限することで、時間領域では振動性になるのはご理解いただけるのでは無いかと思います。
一方、時間領域の補間関数として、C-スプライン関数が知られています。時間領域の信号の“滑らかさ”というか、そういった概念から、フルエンシー理論みたいなものが生まれた訳ですが、これを周波数領域でみるなら、上に述べたように単に“折り返し雑音のお漏らし”でしかありません。
なお、蛇足ですが、最初のフルエンシーは、これをアナログ的な畳み込みで行っていましたが、現在ではディジタル領域での畳み込み(FIRフィルタ)になっています。
一方、正弦波の場合は、逆に時間波形が崩れる事もあり得ます。
周波数領域で見て帯域制限が不十分な、スプライン補間の様なことをした DAC に、20kHz付近の信号が入力されれば、標本化周波数 Fs=44.1[kHz] とすると 24.1[kHz]の 信号が漏れてきます。
事実、これら二つの正弦波を適当な比率で加算したものは、Fs=44.1[kHz] で 20kHzの正弦波をスプライン補間した信号に一致します。
下図は、44.1[kHz] で標本化された 20[kHz]の正弦波をスプライン補間したものです。
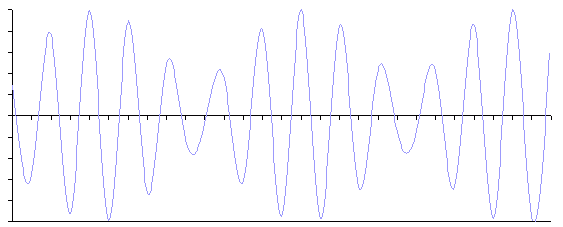
図.5 Fs/2 付近の正弦波のスプライン補間
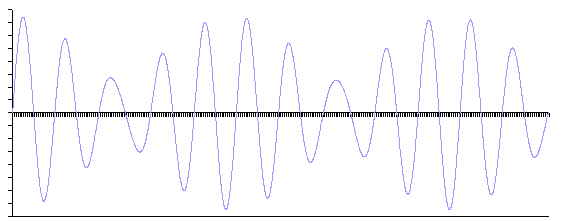
図.6 エイリアスとの加算結果
即ち、明らかに折り返しが問題になる高い周波数では、極めて急峻なフィルタ(つまり sinξ/ξ の補間)でなければ、理論通りの再現はできないと言うことです。
当たり前です。既に述べたように、標本化定理は sinc関数での帯域制限を前提にしているのですから。
時間領域の滑らかさを問題にするか否かは、聴覚心理の問題でしょうが、現在使用されているディジタルフィルタについて言うなら、ある意味「実験的に決着のついた問題」でしょう。
寅市教授のフルエンシー理論は、その後あまり学会でも話題にならないように思います。
ある物理学系のHPで、つまらない理論への学会の反応についての話がありました。要約すると、
“「黙殺」は評価に値しない理論への明確な意思表示です。”
例えば、「聖書の暗号」という有名なトンデモ本があります。
この本の元ネタになった論文を書いた数学者は、「反論が無いのは、この理論が正しいから」みたいな事を匂わせていますが、そうでは無いという事ですね。