1. 凸関数

1. 凸関数
2. Jensenの不等式
3. 算術平均・幾何平均・調和平均
4. 標準偏差と平均偏差

凸関数とは

関数 f(x) の定義域に含まれる任意の a，b と， 0 ≤ t ≤ 1 の範囲に含まれる任意の t に対して \[ f((1-t)a+tb) \le (1-t)f(a)+tf(b) \tag{1} \] が成り立つとき，関数 f(x) は凸関数であるという。

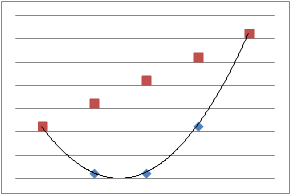
これは a ≤ x ≤ b において関数 y=f(x) のグラフが， 2点 (a,f(a))，(b,f(b)) を結ぶ線分より下側にあるという意味である。 2次関数 y=x²，指数関数 y=e^x 等は凸関数である。

次のページへ

1 2 3 4 Next

2. Jensenの不等式

1. 凸関数
2. Jensenの不等式
3. 算術平均・幾何平均・調和平均
4. 標準偏差と平均偏差

Jensenの不等式

ある区間で定義された f(x) は凸関数で， x₁，x₂，…，x_nは f(x) の定義域に属する数とする。 p₁+p₂+…+p_n=1 を満たす非負の p₁，p₂，…，p_n に対して \[ f(p_1 x_1+p_2 x_2+ \dots +p_n x_n) \le p_1 f(x_1)+p_2 f(x_2)+ \dots +p_n f(x_n) \] が成り立つ。

（証明）

もし p_n=0 となる場合は， p₁，p₂，…，p_n−1 のうち少なくとも1つは正であるから，その番号と n を入れ替えて， p_n>0 となるようにしておく。 定理の左辺を L₁ とおき，次のように変形する。 \begin{align} L_1 &= f(p_1 x_1+p_2 x_2+ \dots +p_n x_n) \\ &= f\left(p_1 x_1 + (p_2+ \dots +p_n)\frac{p_2 x_2+ \dots +p_n x_n}{p_2+ \dots +p_n}\right) \end{align} p₁ と p₂+…+p_n の和は1なので， 凸関数の性質から次の不等式が成り立つ。 \[ L_1 \le p_1 f(x_1)+(p_2+ \dots +p_n) f\left(\frac{p_2 x_2+ \dots +p_n x_n}{p_2+ \dots +p_n}\right) \] 最後の f の部分を L₂ と置き換えて， \[ L_1 \le p_1 f(x_1)+(p_2+ \dots +p_n) L_2,\qquad L_2 = f\left(\frac{p_2 x_2+ \dots +p_n x_n}{p_2+ \dots +p_n}\right) \tag{2} \] L₂ についても上と同じように変形すると， \begin{align} L_2 &= f\left(\frac{p_2 x_2+p_3 x_3+ \dots +p_n x_n}{p_2+ \dots +p_n}\right) \\ &= f\left(\frac{p_2}{p_2+ \dots +p_n} x_2 +\frac{p_3+ \dots +p_n}{p_2+ \dots +p_n} \cdot \frac{p_3 x_3+ \dots +p_n x_n}{p_3+ \dots +p_n}\right) \end{align} p₂/(p₂+…+p_n) と (p₃+…+p_n)/(p₂+…+p_n) の和は1なので， 凸関数の性質から次の不等式が成り立つ。 \[ L_2 \le \frac{p_2}{p_2+ \dots +p_n} f(x_2)+\frac{p_3+ \dots +p_n}{p_2+ \dots +p_n} f\left(\frac{p_3 x_3+ \dots +p_n x_n}{p_3+ \dots +p_n}\right) \] (2)と合わせて次の結果が得られる。 \[ L_1 \le p_1 f(x_1)+p_2 f(x_2)+(p_3+ \dots +p_n) L_3,\qquad L_3 = f\left(\frac{p_3 x_3+ \dots +p_n x_n}{p_3+ \dots +p_n}\right) \tag{3} \] これを繰り返していくと，最後には次のように変形できる。 \begin{align} &L_1 \le p_1 f(x_1)+ \dots +p_{n-2} f(x_{n-2})+(p_{n-1}+p_n) L_{n-1},\\ &L_{n-1} = f\left(\frac{p_{n-1} x_{n-1}+p_n x_n}{p_{n-1}+p_n}\right) \end{align} もう一度凸関数の性質を用いて， \[ L_{n-1} = f\left(\frac{p_{n-1} x_{n-1}+p_n x_n}{p_{n-1}+p_n}\right) \le \frac{p_{n-1}}{p_{n-1}+p_n} f(x_{n-1})+\frac{p_n}{p_{n-1}+p_n} f(x_n) \] これより定理が証明される。 \[ L_1 \le p_1 f(x_1)+p_2 f(x_2)+ \dots +p_n f(x_n) \]

次のページへ

1 2 3 4 Next

3. 算術平均・幾何平均・調和平均

1. 凸関数
2. Jensenの不等式
3. 算術平均・幾何平均・調和平均
4. 標準偏差と平均偏差

3つの平均値の定義

任意の数 x₁，x₂，…，x_nに対して， 算術平均（arithmetic mean） A は次の式で定義される。 相加平均ともいう。 \[ A = \frac{1}{n} \sum_{i=1}^n x_i = \frac{x_1+x_2+ \dots +x_n}{n} \] 非負の数 x₁，x₂，…，x_nに対して， 幾何平均（geometric mean） G は次の式で定義される。 相乗平均ともいう。 \[ G = \left(\prod_{i=1}^n x_i\right)^{\frac{1}{n}} = \sqrt[n]{x_1 \times x_2 \times \dots \times x_n} \] 正の数 x₁，x₂，…，x_nに対して， 調和平均（harmonic mean） H は次の式で定義される。 調和平均は，逆数の算術平均の逆数である。 \[ H = \left(\frac{1}{n} \sum_{i=1}^n {x_i}^{-1}\right)^{-1} = \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+ \dots +\frac{1}{x_n}} \] これら3つの平均値について A ≥ G ≥ H となることが知られている。 そのことを以下に示す。

算術平均と幾何平均

算術平均は幾何平均より常に大きいかまたは等しい（A ≥ G）。 Jensenの不等式を利用してこれを示そう。 正の数 x₁，x₂，…，x_n に対して， x_i の自然対数を y_i とおく。 \[ y_i = \ln x_i = \log_e x_i,\qquad x_i = \exp y_i = e^{y_i} \] 算術平均 A を y_i の式で表すと， \[ A = \frac{1}{n} \sum x_i = \frac{1}{n} \sum \exp y_i \] 幾何平均 G を y_i の式で表すと， \[ G = \left(\prod x_i\right)^{\frac{1}{n}} = \left(\prod \exp y_i\right)^{\frac{1}{n}} = \left(\exp \sum y_i\right)^{\frac{1}{n}} = \exp \frac{1}{n} \sum y_i \] となる。exp(y) は凸関数であるから，Jensenの不等式を用いると \[ \exp \sum \frac{1}{n} y_i \le \sum \frac{1}{n} \exp y_i \] となる。 これらを合わせると， 正の数 x₁，x₂，…，x_n に対して， \[ A \ge G \] となることがわかる。 このことは非負の数 x₁，x₂，…，x_n に対しても成り立つ。 なぜなら，x_i=0 となる数があるときは G=0 かつ A ≥ 0 となるからである。

幾何平均と調和平均

幾何平均は調和平均より常に大きいかまたは等しい（G ≥ H）。 これを示そう。 1/x₁，1/x₂，…，1/x_n に対する算術平均を A'，幾何平均を G' とすると，上の結果から A' ≥ G' である。 A' については \[ A' = \frac{\frac{1}{x_1}+\frac{1}{x_2}+ \dots +\frac{1}{x_n}}{n} = \frac{1}{H} \] G' については \[ G' = \sqrt[n]{\frac{1}{x_1} \times \frac{1}{x_2} \times \dots \times \frac{1}{x_n}} = \frac{1}{\sqrt[n]{x_1 \times x_2 \times \dots \times x_n}} = \frac{1}{G} \] これらを合わせると \[ \frac{1}{H} \ge \frac{1}{G} > 0 \] であるから \[ G \ge H \] となることがわかる。

次のページへ

1 2 3 4 Next

4. 標準偏差と平均偏差

1. 凸関数
2. Jensenの不等式
3. 算術平均・幾何平均・調和平均
4. 標準偏差と平均偏差

標準偏差・平均偏差とは

x₁，x₂，…，x_n に対して，次の値を標準偏差（standard deviation）といい，SD で表す。 μ は平均値とする。 \[ \text{SD} = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i-\mu)^2} \] また，次の値を平均値からの平均絶対偏差（average absolute deviation）といい，AD で表す。 簡単に平均偏差ということもある。μ は平均値とする。 \[ \text{AD} = \frac{1}{n} \sum_{i=1}^n |x_i-\mu| \] 一般に AD ≤ SD となることが知られている。 そのことを以下に示す。

標準偏差と平均偏差の大小

平均偏差は標準偏差より常に小さいかまたは等しい（AD ≤ SD）。 Jensenの不等式を利用してこれを示そう。 x_i と μ の差の絶対値を y_i とおく。 \[ y_i = |x_i - \mu| \] 2次関数 f(y)=y² は凸関数なので，Jensenの不等式を用いると， \[ \left(\sum \frac{1}{n} y_i\right)^2 \le \sum \frac{1}{n} {y_i}^2 \] 左辺は平均偏差の2乗，右辺は標準偏差の2乗であり，どちらも非負数である。 \[ 0 \le \text{AD}^2 \le \text{SD}^2 \] よって \[ \text{AD} \le \text{SD} \] となることがわかる。

最後のページです

1 2 3 4 Home

イェンゼンの不等式

Home  イェンゼンの不等式  シュワルツの不等式